Logarithms and octaves

Previous chapter ( Golden ratio )	Table of contents	Next chapter ( Informatics )

Corresponding Wikipedia article: Logarithm

Definition

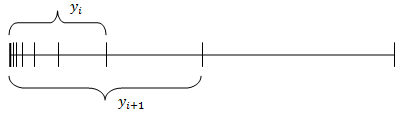
Let a line segment is divided into two parts with any ratio (golden or not). Then a particular part is divided with the same ratio, and so on infinitely. In the example below, a line segment is divided into halves, and then its left part is divided:

The produced segment length sequence \(y_i\) is a simple geometric progression: \[\frac{y_{i+1}}{y_i}=a\] \[\frac{y_{i+n}}{y_i}=a^n\] For this example the common ratio \(a=2\).

This segment system is self-similar, i.e. its parts are similar to the whole, and this whole can be a part of a larger whole. The division of each partial segment as a whole produces a self-similar fractal tree. The figure below shows two levels of this tree:

The progression \(y_i\)is replaced by a continuous function \(y(x)\): \[x=i+\frac{i_1}{N}+\frac{i_2}{N^2}+\dots\] \[y(x)=y_i+\frac{y_{i1}}{N}+\frac{y_{i2}}{N^2}+\dots\] The function \(y(x)\) is defined for an infinitesimally small change of an argument \(\Delta x\) as a simple linear equation: \[\frac{y(x+\Delta x)}{y(x)}=1+k\Delta x\] \[\frac{y(x+n\Delta x)}{y(x)}=(1+k\Delta x)^n\] The unique property of this function derivative is a consequence from its definition: \[\frac{\mathrm{d}y}{\mathrm{d}x}=\lim_{\Delta x\to 0}{\frac{y(x+\Delta x)-y(x)}{\Delta x}}=ky(x)\] Let some interval between two integer values \((i,i+1)\) of an argument \(x\) is divided into n equal parts, and: \[\Delta x=\frac{1}{n}\] If \(n\to\infty\), then \(\Delta x\) becomes infinitesimally small, and the progression common ratio, according to the second remarkable limit, is an exponential function: \[a=\frac{y_{i+1}}{y_i}=\frac{y(x+1)}{y(x)}=\lim_{n\to\infty}{\left(1+\frac{k}{n}\right)^n}=\lim_{n\to\infty}{\left(1+\frac{k}{n}\right)^{\frac{n}{k}k}}=\mathrm{e}^k\] The natural logarithm is an inverse function of an exponential function: \[k=\ln ⁡a\] The logarithm derivative is also defined according to the second remarkable limit: \[\frac{\mathrm{d}\ln ⁡x}{\mathrm{d}x}=\lim_{\Delta x\to 0}{\frac{1}{\Delta x}\ln⁡\left(1+\frac{\Delta x}{x}\right)}=\lim_{\Delta x\to 0}{\frac{1}{x}\ln⁡\left(1+\frac{\Delta x}{x}\right)^\frac{x}{\Delta x}}=\frac{1}{x}\] The logarithm invention has allowed a fractional irrational index of power, which has no such geometric interpretation as has the square or the cube. The fractals and the logarithms also lead to the fractional spatial dimensionality.

Logarithmic scale

The logarithmic scale requires any conventional reference point \(y_0=y(0)\), to convert the relative values into the absolute physical values: \[y_i=y_0 ⁡a^i\] \[y(x)=y_0 ⁡a^x=y_0 ⁡\mathrm{e}^{kx}\] \[\frac{\ln(y/y_0)}{\ln a}=\log_a{\frac{y}{y_0}}\] The octave is an interval of the oscillation frequency scale, which is divided into octaves in a geometric progression with a common ratio 2. The binary (to the base 2) logarithm can define an octave number by its integer part, and its fractional part defines a tone inside the octave scale, which is repeated cyclically from one octave to another.

The logarithms are related to the various laws of the living nature:

Logarithmic scale	Description
Sound pitch	The reference point is any conventional frequency. The octave is defined unambiguously. It’s known a few tone scale modes inside the octave: the pentatonic, diatonic and chromatic scale.
Sound duration	The information is contained not in the music tempo or in the speaking rate, but in a ratio of the sound durations. The scale of the musical note values is a geometric progression with a common ratio 2.
Sound volume (loudness)	The reference point is an average hearing threshold. A quiet sound seems to be louder due to the logarithms. The sound pressure spatial decay is nearly proportional to the square of the distance to a sound source, but feels like a linear dependence.
Brightness	A dark light seems to be brighter due to logarithms. The brightness spatial decay is nearly proportional to the square of the distance to the light source, but feels like a linear dependence.

Golden ratio

The relationship of a natural logarithm with the Fibonacci sequence and the “golden numbers”\[\ln\sum_{i=0}^{N-1}{F_i}\approx\frac{N}{2}\]

\(N\)	\(\sum_{i=0}^{N-1}{F_i}\)	\(\ln\sum_{i=0}^{N-1}{F_i}\)	error
3	4	1,386	8%
4	7	1,946	3%
5	12	2,485	0,6%
6	20	2,996	0,1%
7	33	3,497	0,3%
8	54	3,989	0,3%
9	88	4,477	0,5%
10	143	4,963	0,7%

See also

• Image

---

Previous chapter ( Golden ratio )	Table of contents	Next chapter ( Informatics )