Helix and spiral
| Previous chapter ( Vortex ) | Table of contents | Next chapter ( Ring ) |
Corresponding Wikipedia article: Helicoidal flow
A simple condition of a steady-state vortex follows from the equation ("Vortex", 7): \[\mathbf{\overrightarrow{v}}\times curl\,\mathbf{\overrightarrow{v}}=0\tag{1}\] \[curl\,\mathbf{\overrightarrow{v}}=k\mathbf{\overrightarrow{v}}\tag{2}\] The flow with such condition looks like a helix (spiral) called the Beltrami or ABC (Arnold-Beltrami-Childress) flow. The helical flow, regardless of the listed authors, was better described in details by Gromeka[1].
The obvious properties of a helical flow are:
- The vortex lines are matching the streamlines (vectors are collinear).
- The constant in Bernoulli's law is the same over entire continuum, that is, the same Bernoulli's equation is valid over any line. This follows from the Gromeka-Lamb equation ("Vortex", 3).
For an uniform helical flow (\(k=const\)), the condition (2) subjected to the curl operator and the known formula of vector analysis becomes: \[curl\;curl\,\mathbf{\overrightarrow{v}}=k\;curl\,\mathbf{\overrightarrow{v}}\tag{3}\] \[grad\;div\,\mathbf{\overrightarrow{v}}-\Delta\mathbf{\overrightarrow{v}}=k^2\mathbf{\overrightarrow{v}}\tag{4}\] Hence, the Helmholtz wave equation is valid for a steady-state vortex (\(div\,\mathbf{\overrightarrow{v}}=0\)) of the incompressible or barotropic flow: \[\boxed{\Delta\mathbf{\overrightarrow{v}}+k^2\mathbf{\overrightarrow{v}}=0}\tag{5}\] This elliptic equation has many solutions, which describe something like a wave with wavenumber \(\approx k\), which propagates with arbitrary velocity including zero. Such wave is called the soliton.
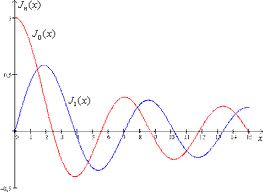
For a helical flow along one axis, Gromeka had found a simple solution in the cylindrical coordinates \((r,\theta,z) \)[1]:
\[v_r=0\]
\[v_\theta=CJ_1(kr)\]
\[v_z=CJ_0(kr)\]
where \(C\) is a constant, which depends on the fluid discharge;
\(J_0, J_1\) is the Bessel functions of 1st kind.
The given example shows that the flow velocity not only decreases with distance from the vortex axis, but it can also change own direction.
The Ranque-Hilsch tube shows the effect of the direction change. The fast cold air is directed to one side from the vortex center, and the slow hot air to the opposite direction from the vortex periphery.
The optimal twisting angle can minimize the flow velocity at the pipe walls, reducing the friction loss. Here are the examples:
- Flow twisting in the aorta reduces the heart workload.
- Helicoid, a helical profile pipe with the minimum flow resistance, which repeats the river bed shape, as the inventor V. Schauberger explains.
See also
References
- ↑ 1.0 1.1 Громека И.С., Некоторые случаи движения несжимаемой жидкости (докторская диссертация), Отд. изд. Казань, 1881, 107 стр.; Громека И.С., Собрание трудов, Москва: АН СССР, 1952, с.76-148.
| Previous chapter ( Vortex ) | Table of contents | Next chapter ( Ring ) |