Electric field and Lorentz force
| Previous chapter ( Magnetic energy ) | Table of contents | Next chapter ( Charge and Coulomb's law ) |
Corresponding Wikipedia articles: Electric field, Lorentz force
The quantity of the electric field is similar to the magnetic field and is divided into the cause and the effect:
- Cause. The electric field \(\mathbf{\overrightarrow{E}}\) as a ratio of the electric force to the electric charge.
- Effect. The electric displacement \(\mathbf{\overrightarrow{D}}\), which depends on the matter response to the electric forces action.
| SI | CGS | Simplified | \(\tag{1}\) |
|---|---|---|---|
| \[\mathbf{\overrightarrow{E}}=\frac{\rho\mathbf{\overrightarrow{f}}}{q}=\frac{\mathbf{\overrightarrow{F}}}{Q}\] | \[\mathbf{\overrightarrow{E}}=\frac{\varepsilon\rho\mathbf{\overrightarrow{f}}}{q}=\frac{\mathbf{\overrightarrow{F}}}{Q}\] | ||
| \[\mathbf{\overrightarrow{D}}=\varepsilon_0\varepsilon\mathbf{\overrightarrow{E}}\] | \[\mathbf{\overrightarrow{D}}=\varepsilon\mathbf{\overrightarrow{E}}\] | \[\tag{2}\] | |
| \(\varepsilon_0\) is a permittivity of the vacuum, \(\varepsilon\) is a relative permittivity of the medium (\(\varepsilon=1\) in the vacuum). | |||
The field is a sum of the static and dynamic (vortical) components with the superposition of multiple sources.
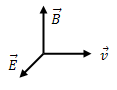
The electric field quantity follows from ("Electricity", 5): \[\mathbf{\overrightarrow{E}}=\mathbf{\overrightarrow{v}}\times\mathbf{\overrightarrow{B}}\tag{3 – SI, Sim.}\] \[\mathbf{\overrightarrow{E}}=\frac{\mathbf{\overrightarrow{v}}}{c}\times\mathbf{\overrightarrow{B}}\tag{3 – CGS}\] The vector directions are defined by the left-hand rule or the right system \((\mathbf{\overrightarrow{E}},\mathbf{\overrightarrow{v}},\mathbf{\overrightarrow{B}})\):
The electrostatic field of the material particles is produced by the motion of their aether with respect to the object, on which this field acts. The relative aether velocity depends on the object velocity, affecting the electric field value by (3), but this effect is compensated by the Lorentz force, which has the same nature and value. So, for example, the Lorentz force is not included into the Bohr atomic theory, where the electron spins within the nucleus magnetic field.
The Lorentz force, which acts on a point charge \(Q\), is: \[\mathbf{\overrightarrow{F}}=Q\mathbf{\overrightarrow{E}}=Q\mathbf{\overrightarrow{v}}\times\mathbf{\overrightarrow{B}}\tag{4 – SI, Sim.}\] \[\mathbf{\overrightarrow{F}}=Q\mathbf{\overrightarrow{E}}=Q\frac{\mathbf{\overrightarrow{v}}}{c}\times\mathbf{\overrightarrow{B}}\tag{4 – CGS}\] The velocity \(\mathbf{\overrightarrow{v}}\) for the Lorentz force is determined with respect to the magnetic field source. For example, the Faraday disc has two operational designs:
- Motionless magnet and the disk rotating in its field.
- Magnetic rotating disk.
The energy volumetric density of the electric field is defined similarly to the magnetic energy definition (see "Magnetic energy"):
| SI | CGS | Simplified | \(\tag{5}\) |
|---|---|---|---|
| \[w_E=\frac{\mathbf{\overrightarrow{D}}\mathbf{\overrightarrow{E}}}{2}=\frac{\varepsilon_0\varepsilon|\mathbf{\overrightarrow{E}}|^2}{2}\] | \[w_E=\frac{\mathbf{\overrightarrow{D}}\mathbf{\overrightarrow{E}}}{8\pi}=\frac{\varepsilon|\mathbf{\overrightarrow{E}}|^2}{8\pi}\] | \[w_E=\frac{\mathbf{\overrightarrow{D}}\mathbf{\overrightarrow{E}}}{2}=\frac{\varepsilon|\mathbf{\overrightarrow{E}}|^2}{2}\] |
The potential energy volumetric density of the electric interaction is: \[w=\mathbf{\overrightarrow{D}}\mathbf{\overrightarrow{E}}\tag{6}\] The minimal potential energy is produced by the field neutralization. Thus, the different charges attract each other, and the same charges repel each other.
The electric interaction force is asymmetric and weakened at the vortex axis, giving advantage to the magnetic attraction, which causes the pairing of the same charged elementary particles.
The electric force asymmetry is smoothed due to a large number of the charged particles and their thermal chaotic motion.
| Previous chapter ( Magnetic energy ) | Table of contents | Next chapter ( Charge and Coulomb's law ) |