Atom
| Previous chapter ( Nucleus ) | Table of contents | Next chapter ( Fine-structure constant ) |
Corresponding Wikipedia article: Atom
Contents
Introduction
The atoms are composed of the electrons and the nuclei, the interaction of which is subject to the electromagnetic and mechanical laws.
The electron shells of the molecular and heavy nuclei are formed by the sedentary paired electrons, which are uniformly distributed by the forces of mutual electrostatic repulsion. The internal electrons of the heavy atoms are overlapped with the nucleus and are capturing by it with a high probability.
The existing scientific knowledge on the atom is mainly based on a visual observation of the absorption and emission spectrums.
Hydrogen spectrum
An excited electron rotates around the nucleus, and the centrifugal force balances the electrostatic attraction. In the well-known equation for a hydrogen, the additional gravitational correction \((1+z)\) causes a red shift of the spectrum: \[\frac{m_ev^2}{r}(1+z)=\frac{e^2}{4\pi\varepsilon_0r^2}\tag{1}\] The nuclear field with a non-uniform (wave) density distribution can be represented as a system of the concentric rotating bodies, which shape the interchanging dense and sparse layers. The De Broglie waves, which are scattered by the electrons, are able to remain within the nuclear field, moving on the circular paths of the small radii, flowing around the dense layers, like a liquid or a gas, which flows around a solid body. The circular motion of the beam causes the interference, the maximum of which occurs only when the path circumference length is multiple of the de Broglie wavelength. With other circumference length, the beam is attenuated at each turn. The annular beam path is close to the electron orbit, and the non-attenuated beam returns most of the scattered electron energy back to the electron, so the corresponding orbit is much more stable than others, and it is called the allowed orbit. The electron on the non-allowed orbits without the external energy sources begins to lose own speed and reduces own orbit. The elliptical orbits are not supported also.
The electron de Broglie wavelength is: \[\lambda=\frac{h}{m_ev}\tag{2}\] In the ideal case, when the external electromagnetic fields do not exist, and when the atoms interact weakly with each other, having almost spherical shape of their fields, the beam paths are matching the circular orbits of the electrons. The gases and plasma, in which the quantum spectral effects are observed, are related to this case, when the condition of multiplicity of the path lengths and the wavelengths has the following form: \[\lambda_n=\frac{2\pi r}{n}\;\;\;\;\;n=1,2,\dotsc\tag{3}\] The condition (3), when expressed by the angular momentum, becomes the 1st Bohr's postulate. For the hydrogen atom, the velocities and radii of the allowed orbits have the values, which are known from the Bohr’s theory: \[v_n=\frac{e^2}{2\varepsilon_0hn}\frac{1}{(1+z)}\approx\frac{2,2\cdot 10^6}{n(1+z)} м/с\tag{4}\] \[r_n=\frac{\varepsilon_0h^2}{\pi m_ee^2}n^2(1+z)\approx n^2(1+z)\cdot 5,3\cdot 10^{-11} м\tag{5}\] The energy levels are combined from the kinetic energy (gravity-adjusted) and the electrostatic potential energy: \[W_{Kn}=\frac{m_ev^2}{2}(1+z)=\frac{m_ee^4}{8\varepsilon_0^2h^2n^2}\frac{1}{(1+z)}\tag{6}\] \[W_{Pn}=-\frac{e^2}{4\pi\varepsilon_0r_n}=-\frac{m_ee^4}{4\varepsilon_0^2h^2n^2}\frac{1}{(1+z)}\tag{7}\] \[W_{n}=W_{Kn}+W_{Pn}=-\frac{m_ee^4}{8\varepsilon_0^2h^2n^2}\frac{1}{(1+z)}\approx-\frac{13,6}{n^2(1+z)}эВ\tag{8}\] During the electron transition from a high level to a low level, only one half of its electrostatic potential energy is converted into the electron kinetic energy, and the other half into the radiation.
The ratio of the excited electron speed in a hydrogen atom (\(n=1\)) to the speed of light is called the fine-structure constant: \[\alpha=\frac{e^2}{2\varepsilon_0hc}\approx\frac{1}{137}\tag{9}\] The fine structure of the spectral line is its splitting into several closely spaced discrete lines. When the de Broglie wave turns around its orbit \(l\) times, the electron passes an orbital segment of length \(\alpha l\). The running wave is moving on the same orbit as the electron. The quantization condition depends on a small integer value \(l\): \[\lambda_nn=2\pi r(1+\alpha l)\tag{10}\] \[W_{nl}\approx W_n\left(1+2\frac{\alpha l}{n}\right)\tag{11}\]
Multi-electron atomic spectrum
The multi-electron excited atoms have a more complicated level structure due to the electrons interactions, such as:
- Pairing, which produces the kinetic energy consumption to destroy the bonds.
- Screening (shielding) is a partial neutralization of the nuclear electric charge by the surrounding electrons.
There are the discrete (quantum) states within any main (principal) energy level \(n\), which are called the sub-levels or the states with various azimuthal (orbital) quantum numbers. The quantum mechanics claims, that the smaller the azimuthal (orbital) number \(l=0,1,\dotsc,n-1\) is, the lower is actual energy level. The quantum mechanics also defines the empirical "quantum defect" for each atom and each azimuthal (orbital) number.
| Quantum mechanics | Aether mechanics | |
|---|---|---|
| Number | State | |
| 0 | S (sharp) | Paired electron. The destruction of bond consumes energy and reduces the energy level. The excited pairs are destroying with a sharp transition, usually to the P-state. |
| 1 | P (principal) | Most probable case of a single electron, which is surrounded by other similar ones. Most probable transition is to the S-state with minimum energy. The energy consumption for the spontaneous creating-destroying of the unstable pairs causes the level splitting during the transitions. |
| 2 | D (diffuse) | Less probable case of a single electron with high energy. The screening (shielding) of the nuclear charge and the energy levels are high, similarly to the hydrogen atom, especially for the F-state. |
| 3 | F (fundamental) | |
The electrons don't interact in the excited hydrogen atom. The quantum mechanics calls this the degeneracy.
Influence of external fields on spectrum
The Stark effect is a splitting of the energy level within the external electric field and also within molecules and crystals. The level shifting is related to the potential energy of the external field.
The Zeeman effect. The particle radiation intensity depends on a projection of the magnetic flux density at the radiation direction.
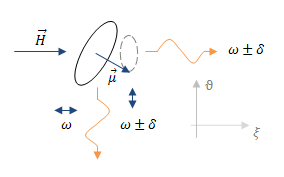
An external magnetic field \(\mathbf{\overrightarrow{H}}\) causes the gyroscopic precession of the electron as of the rotating mass. The fluctuations in the magnetic field with respect to the motionless axes produce the amplitude modulation of radiation along these axes. The axis \(\xi\) is directed along \(\mathbf{\overrightarrow{H}}\), and the axis \(\vartheta\) in arbitrary perpendicular to the \(\mathbf{\overrightarrow{H}}\) direction.
The model of the electron radiation in a form of its magnetic component \(B(t)\) in the coordinate plane \((x,y)\), which is perpendicular to the radiated beam, is:
\[B_x(t)=B_0(a_{x\xi}+2a_{x\vartheta}\cos\delta t)\cos\omega t\]
\[B_y(t)=B_0(a_{y\xi}+2a_{y\vartheta}\sin\delta t)\cos\omega t\]
where \(B_0\) is a value, which depends on the radiation energy;
\(a_{x\xi}, a_{x\vartheta}, a_{y\xi}, a_{y\vartheta}\) are the factors, which depends on the radiation direction;
\(\delta\) is an angular frequency of precession;
\(\omega\) is an angular frequency without the Zeeman effect.
The radiation along \(\mathbf{\overrightarrow{H}}\) is modulated only by the AC component of the field \((a_{x\xi}=a_{y\xi}=0,\;a_{x\vartheta}=a_{y\vartheta}\neq 0)\) and consists of two beams with different frequencies and with a circular polarization in different rotation directions: \[B_x(t)=B_0a_{x\vartheta}(\cos(-(\omega-\delta)t)+\cos(\omega+\delta)t)\] \[B_y(t)=B_0a_{y\vartheta}(\sin(-(\omega-\delta)t)+\sin(\omega+\delta)t)\] The radiation across \(\mathbf{\overrightarrow{H}}\) with y-axis oriented along \(\mathbf{\overrightarrow{H}}\) (axis \(\xi\)), and \(\vartheta\) along \(x\), has the factors \(a_{x\xi}=0,\;a_{y\xi}\neq 0,\;a_{x\vartheta}\neq 0,\;a_{y\vartheta}\approx 0\). Neglecting \(a_{y\vartheta}\), the radiation consists of three beams with different frequencies and with a linear polarization in the orthogonal directions: \[B_x(t)=B_0a_{x\vartheta}(\cos(\omega-\delta)t+\cos(\omega+\delta)t)\] \[B_y(t)=B_0a_{y\xi}\cos\omega t\]
| Previous chapter ( Nucleus ) | Table of contents | Next chapter ( Fine-structure constant ) |